This project is one my space related personal projects. The current status of this project is work in progress.
{Abstract goes here.}
This paper is still not complete! However, there is enough material present that a dedicated reader (perhaps you?) can probably figure out what I am talking about.
The concept of developing asteroid resources has been around for many years. One of the best early treatments of asteroid development can be found in the book Islands in Space: The Challenge of the Planetoids by Cole and Cox published in 1964 [Cole1964]. The Cole and Cox bibliography cites even earlier references to the concept of asteroid development. NASA appears to have gotten around to looking into the idea of asteroid development when Dr. Gerald K. O'Neill popularized the idea of space colonies. Several papers on asteriod resource development appeared in NASA SP-428, Space Resources and Space Settlements [Bender1979] [Gaffey1977] [O'Leary1977]. The relevant papers in NASA SP-428 examine the possibility of using Earth, Moon, & Venus orbital assists to reduce the total amount of momentum exchange (aka delta V) required to visit and return from near earth asteroids. One of the more recent advocates of asteroid development has been Prof. John Lewis of the University of Arizona who has written a book entitled Mining the Sky [Lewis1996].
Over a period of time, a theory has evolved that a significant number of the near earth asteroids (NEA) are, in fact, comets that have developed an outer coating that prevents subsequent out-gassing of cometary gases. The following quote from Short Period Comets by Weissman and Campins [Weissman1993] is a pretty concise summary of the theory:
Of particular interest with respect to space exploration of comets is the formation of nonvolatile crusts on the nucleus surfaces. As discussed above, all nuclei studied to date show evidence that a substantial fraction of their surfaces are covered by an inert crust. In essence, these crusts greatly extend the physical lifetimes of the comets by preventing the sublimation of cometary ices. In addition, the crust may eventually totally cover the nucleus surface making the comet appear to be a dormant, asteroidal object. This leads to the interesting possibility the some of the Earth-crossing and Earth-approaching asteroids may in fact be extinct cometary nuclei which have been totally covered over by a nonvolatile crust. A number of theoretical models have been developed in which an inert crust, a few centimeters to perhaps a meter in thickness, builds up on the surface of the nucleus, reducing or stopping the sublimation of ices.A diagram of what the cross section such a comet/asteroid might look like is taken from the same paper and shown below:
If this theory of asteroids is true, there is good reason to believe that there are numerous near earth asteroids that have an inner core that is rich in volatiles, particularly water. This theory will not be validated until we get some space probes out to some near earth asteroids with some neutron spectrometers to detect the presence of hydrogen. However, it is not too premature to speculate on how to use these volatiles if they turn out to be present.
The rest of this paper speculates about a solar transportation system for moving matter around the solar system using water mined from extraterrestrial sources such as near earth asteroids.
Historically, moving materials around the solar system has been done using Hohmann transfer orbits and sling-shot maneuvers past moons and planets. A Hohmann transfer orbit is an elliptical orbit that connects two coplanar circular orbits. A simple diagram of a Hohmann transfer orbit is shown below:
The following quote from Fundamentals of Astrodynamics by Bate, Mueller and White [Bate1971] summarizes the advantages and disadvantages of Hohmann transfer orbits:
While the Hohmann transfer is the most economical from the standpoint of delta-V required, it also takes longer than any other possible transfer orbit between the same two circular orbits.Hohmann transfer orbits minimize the mass and energy expenditure for transferring between circular orbits (in the same plane) at the expensive requiring approximately half an orbital revolution to accomplish the task. When you are paying $25K/kg. to reach low earth orbit, Hohmann transfer orbits and sling-shot maneuvers are an economic necessity. However, in a solar transportation system where the reaction mass is mined from extraterrestrial sources, it may make sense to use additional reaction mass to reduce transit time and minimize the amount of time an expensive transport is spending `in transit'.
It is easy to come up with an uneconomical solar transportation system that requires government subsidies to operate. I am more interested in a solar transportation system that is economical (i.e. it can pay its own way without government subsidies.) The costs of a solar transportation system can be broken into three broad categories:
When analyzing the solar transportation system economics, it is important to consider the time value of money. If you have a transport that costs N million dollars, and it can make one useful round trip in 24 months, the N million dollars is tied up for the duration of the entire trip. However, if you have a system that N million dollar transport can make 4 useful trips in the same 24 months, the system is N million dollars is only tied up for an average of 6 months per trip.
There are two modes of operation that come to mind:
Over the years a number of different solar transportation systems have been proposed and investigated. A short list of some of the more popular ones are listed below:
The transportation system described below is based on using water mined from an extraterrestrial source as a reaction mass. This extraterrestrial water can come from either the lunar poles or from near earth asteroids. There is no attempt in this system to minimize the amount of water or mass utilized. If using twice as much water gets the job done in half the time, and it makes economic sense, then so be it.
Water makes a fine and dandy reaction mass for moving around the solar system. There seems to be plenty of it and it is fairly easy to work with. I remain unconvinced that using electrolysis to separate water into H2 and O2 and then reburning it is the way to move around the solar system. 2H2 and 2O2 seem to be appropriate high energy fuels for getting into and out of deep gravity wells, but for moving around the solar system I think we should just leave the water intact and figure out other ways of getting the most push we can out of it.
Immediately below is a rough diagram of something I call a `Spinning Bar Water Thruster':
The spinning bar water thruster consists of a bar that is spun end over end around its center. Two nozzles are attached to each end and they point in the same direction as the axis of rotation. The spinning bar is attached to the water tank via a low pressure slip seal. As the water enters the spinning bar, the centripetal force causes it to be pressurized. The high pressure water is expanded through a nozzle to generate thrust.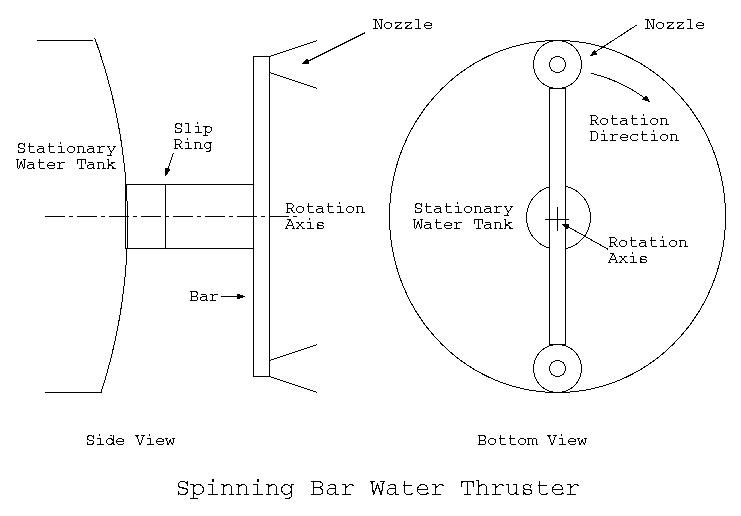
The equation for the pressure at the exit of the bar as a function is:
(1) PBout = PBin+.5*rho*V2where
The exit velocity is basically derived from Bournuelli's equation:
(2) PNin + .5*rho*VNin = PNout + .5*rho*VNoutwhere
VNout = (2*PNin/rho).5Vout is converted to Isp by dividing by gc (i.e. 9.8m/sec2.)
By taking equations (1) and (2) together and setting PBout equal to PNin we get:
(3) VNout = (2*(PBin+.5*rho*V2)/rho).5If we make one more assumption, namely that PBin is much less than the pressure as a result of the bar spinning (i.e. .5*rho*V2), equation 3 simplifies to:
(4) VNout = V
{I still need to do the analysis of what to make the bar out of to maximize V. That analysis belongs right here.}
In conclusion, what this means is that the exit velocity of the water stream is pretty much equal to the tip speed of the spinning bar. Additional exit velocity can be obtained by increasing the pressure at the bar inlet (i.e. PBin), but the additional incremental exit velocity will only go up as the square root of the bar inlet pressure.
{This section is all over the place. It needs to be rearranged and made more coherent.}
The way the entire spinning bar system works is that the bar is spun up to speed, the water is pumped through it, momentum is transfered from the bar to the water which causes it to exit at a nice clip. If energy is not injected into keeping the bar spinning, it will eventually slow down to no rotation. For now, I stipulate that an electric motor is used to keep the bar spinning. So where does the energy to run the motor come from? Well, pretty obviously from solar panels.
The system diagram for the spinning bar water thruster looks as follows:
The solar energy is converted to electrical energy which is converted to mechanical energy via the motor. In addition, some solar energy is used to preheat the water. A small pump is used to move the water from the water tank to the spinning bar. If additional performance is desired, a larger pump can be used.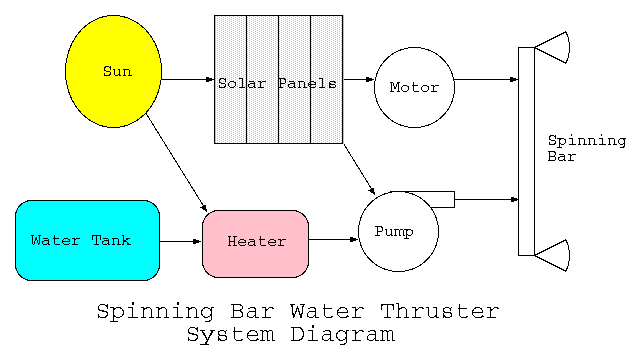
Why the heater? Well, as the water is expanded in the nozzles at the end of the spinning bar, the temperature will drop. If the water is not preheated there is a serious risk that the water could freeze and clog the nozzle. While an electric heater could be used, it is thermodynamically more efficient to directly use the Sun as the heat source. A solar heater can be as simple as a curved piece of shiny mylar reflecting the Sun on to a heating tube as shown below:
Now that the water is being preheated, there is actual energy being extracted from the water as it expands against the nozzle. This results in some additional thrust. This additional thrust can be used to help keep the bar spinning by tilting the nozzles a little. This results in a somewhat smaller motor being needed. The temperature to preheat the water to is primarily limited by the melting points of the materials being used. If you are willing to go towards active cooling, the temperatures can be raised up to the same temperatures as used in regular liquid rocket engine combustion chamber. Of course, active cooling added both mass and complexity to the system.
What about the tanks? Since this is a solar transportation system, tanks can be made out of inflatable bladders. The material does not need to be that thick, it just has to be thick enough to keep the water on one side and the vacuum on the other. The pressure in the tank can be between .5 and 1 atmospheres.
In order to prevent some strange sloshing movements in the tank, it will probably be necessary to attach some guy wires with small motors to the tank rims to keep the tank in a more or less regular shape. Care is needed to ensure that the water does not freeze. This can be accomplished by making one side of the tank shiny (or white) and the other side dark (or black). When the water is getting close to freezing, the dark side of the tank can be pointed at the Sun; conversely, when the the water is getting too close to boiling, the shiny side can be pointed at the Sun.
{I am really unhappy with the state of this summary. There needs to be separate discussion section too.}
The spinning bar water thruster is an exercise in compromises. The overall goal is to have an economical system. Thrusters based around nuclear technology will have higher specific impulses at substantially higher research and development costs. The spinning bar system can quite literally be tested out in somebody's garage. It is also possible to design an engine that will use electrolysis to separate water into hydrogen and oxygen and then reburn the two gases to get thrust. There is fair amount of complexity required for the pumps and for the combustion chamber cooling. Ion engines have terrific specific impulses, but their overall thrust levels are quite small.
{Currently, there is no reference to [Lewis1993]. That needs to be fixed.}