This is the Revision A verion of the Compass360 RoboBrick. The status of this project is that it has been replaced by the revision B version.

Compass360 Robobrick (Revision A)

This document is also available in PDF format.

1. Introduction
2. Programming
3. Hardware
- 3.1 Circuit Schematic
- 3.2 Printed Circuit Board
4. Software
5. Issues
A. Appendix - Designing the Amplifiers

1. Introduction

The Compass360 RoboBrick uses a 1625 analog compass module from Dinsmore Instrument Company to detect magnetic bearing with a resolution approximately 10 bits. You should be informed that the magnetic enviroment inside dwellings can induce substantial errors in magnetic bearing of more than 10 degrees. (You have been warned!)

2. Programming

There is no programming specification yet.

3. Hardware

The hardware consists of a circuit schematic and a printed circuit board.

3.1 Circuit Schematic

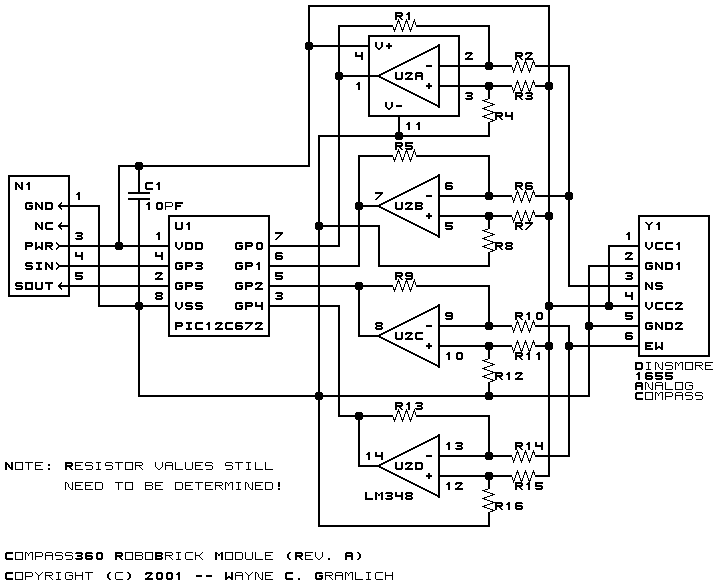
The schematic for the Compass360 RoboBrick is shown below:

The parts list kept in a separate file -- compass360.ptl.

3.2 Printed Circuit Board

The printed circuit board files are listed below:

compass360_back.png: The solder side layer.
compass360_front.png: The component side layer.
compass360_artwork.png: The artwork layer.
compass360.gbl: The RS-274X "Gerber" back (solder side) layer.
compass360.gtl: The RS-274X "Gerber" top (component side) layer.
compass360.gal: The RS-274X "Gerber" artwork layer.
compass360.drl: The "Excellon" NC drill file.
compass360.tol: The "Excellon" tool rack file.

4. Software

There is no software yet.

5. Issues

The following issues have come up:

The input signals should go to plus inputs, not the minus inputs. (I.e. they are swapped.)
There needs to be a 1 volt adjustment voltage fed into the minus input, not Vcc.
The revision A brick is mislabeled as ANALOGIN4-A and should be labeled COMPASS360-A.
Make the holes for N1 (size 3) smaller (size 2).

A. Appendix - Designing the Amplifiers

A1. Basic Amplifier Equations

In order to understand how the resistors around the operational amplifiers are picked it is necessary to analyze one of the amplifier cicuits. We'll do the analysis the amplifier below:

Let's call V_in the input voltage to R₃ and V_adj the adjustment voltage input to R₁.

V₊ is the voltage input to the positive side of the operational amplifier and V_- is the input to the negative side. The trick with operational amplifiers is that they have very high input impedances; hence, the current into and out of both the V₊ and V_- terminals is assumed to be zero. In addition, since we have a properly designed feedback circuit, the operational amplifier will work like crazy to keep V₊ and V_- equal to one another; thus, we just assume that V₊ is always equal to V_-. These assumptions are summarized as:

(1) V₊ = V_-

(2) I_V₊ = 0

(3) I_{V_-} = 0

R3 and R4 form a simple voltage divider of V_in:

(4) V₊ = V_inR₄/(R₃ + R₄)

The voltage drop across R₁ is:

(5) V_R₁ = V_adj - V_-
= V_adj - V₊
= V_adj - V_inR₄/(R₃ + R₄)

Using Ohm's law, we can compute the current through R₁ as:

(6) I_R₁ = V_R₁ / R₁
= [V_adj - V_inR₄/(R₃ + R₄)] / R₁
= V_adj/R₁ - V_inR₄/[R₁(R₃+R₄)]

Since there is no current into V_-, the current through R₂ is the same as the current through R₁:

(7) I_R2 = I_R₁

The voltage drop across R₂ is computed using Ohm's law as:

(8) V_R₂ = I_R₂R₂
= I_R₁R₂ =
= [V_adj/R₁ - V_inR₄/[R₁(R₃+R₄)] ]R₂
= V_adjR₂/R₁ - V_inR₂R₄/[R₁(R₃+R₄)]

The voltage out (V_out) is:

(9) V_out = V_- - V_R₂

= V₊ - V_R₂
= V_inR₄/(R₃ + R₄) - [V_adjR₂/R₁ - V_inR₂R₄/[R₁(R₃+R₄)] ]
= V_inR₄/(R₃ + R₄) - V_adjR₂/R₁ + V_inR₂R₄/[R₁(R₃+R₄)] ]
= V_inR₄/(R₃ + R₄) + V_inR₂R₄/[R₁(R₃+R₄)] - V_adjR₂/R₁
= V_in[R₄/(R₃ + R₄) + R₂R₄/[R₁(R₃+R₄)] ] - V_adjR₂/R₁
= V_in[R₄/(R₃ + R₄) + (R₂/R₁)×R₄/(R₃+R₄)] - V_adjR₂/R₁
= V_in[R₄/(R₃ + R₄) × (1 + R₂/R₁)] - V_adjR₂/R₁
= V_in[(1 + R₂/R₁) × R₄/(R₃ + R₄)] - V_adjR₂/R₁

The equation can be rewritten as:

(10) V_out = V_in × G - V_off

where the amplifier gain is G:

(11) G = (1 + R₂/R₁) × R₄/(R₃ + R₄)

and the voltage offset is V_off:

(12) V_off = V_adjR₂/R₁

A2 Initial Resistor Values

For the first iteration of resistor values, we want the amplifier to take the voltage output from the Dinsmore 1655 analog compass module of 1.9 to 3.1 volts and convert that to a voltage swing of 0 to 5 volts (V_cc).

Let V_low lowest input voltage and V_high be the hight input voltage. What we want is:

(13) V_out = (V_in - V_low)[V_cc/(V_high-V_low)]
= V_in[V_cc/(V_high-V_low)] - V_low[V_cc/(V_high-V_low)]

Matching to equation (13) to equation (10) in the previous section, the gain (G) is:

(14) G = V_cc/(V_high-V_low)

and the voltage offset (V_off) is:

(15) V_off = V_low[V_cc/(V_high-V_low)]

Starting with the voltage offset:

(16) V_off = V_low[V_cc/(V_high-V_low)]
= 1.9 [ 5 / (3.1 - 1.9) ]
= 1.9 ( 5 / 1.2 )
= 1.9 × 4.17
= 7.92

Now combining equations (16) and (12) from the previous section, we get:

(17) V_off = V_adjR₂/R₁

At this point we have to pick a value for V_adj. Initially, I tried to set V_adj to V_cc, but when I worked through the equations, R4 had a negative value. Since I can not buy negative resistor values, I decided to drop V_adj down a little. At V_adj equal to 2.5 volts, it started to work. I ultimately decided to set V_adj to 1 volt because I liked how the numbers worked out a little better.

Now substituting in values for V_off and V_adj we get:

(18) 7.92 = 1 × R₂/R₁

(19) R₂/R₁ = 7.92

I'll pick R₁ to be 100K Ohms thereby getting:

(20) R₂/100K = 7.92

(21) R₂ = 792K

We'll round that down to 750K Ohms.

Now switching over to the gain side of the equation:

(22) G = V_cc/(V_high-V_low)
= 5 / (3.1 - 1.9)
= 5 / 1.2
= 4.17

Now combining equation (22) with equation (11) from the previous section, we get:

(21) G = (1 + R₂/R₁) × R₄/(R₃ + R₄)

and substituting for G, R₁ and R₂ we get:

(22) 4.17 = (1 + 750K/100K) × R₄/(R₃ + R₄)
= (1 + 7.5) × R₄/(R₃ + R₄)
= 8.5 × R₄/(R₃ + R₄)
(23) .49 = R₄/(R₃ + R₄)

Rounding .49 to .5, and picking R₄ to be 100K, we can trivially solve for R₃ to also be 100K.

(24) R₃ = 100K

Thus the final values are:

R₁ = 100K Ohms
R₂ = 750K Ohms
R₃ = 100K Ohms
R₄ = 100K Ohms
V_adj = 1 Volt